執筆者:大和田 克 (Writer:Owada Suguru)
本シリーズは日々ユーザー様より頂戴するご質問のうち、多く頂戴するものや他のユーザー様にも関係し得るものについて、コラム形式で解説・返答するものです。今回のお題は…
Q.NPMで表示されているベータは何時点分のリターンの推定値か?
今回のポイント
1.ベータはどのように定義されるか
ベータはCAPMモデル
$$r_{i,t}-r_{f,t}=\beta_{iM}(r_{M,t}-r_{f,t})+\varepsilon_{i,t}$$
において個別銘柄の超過リターン(無リスク金利調整後リターン) \(r_{i,t}^e=r_{i,t}-r_{f,t}\) の市場ポートフォリオの超過リターン \(r_{M,t}^e=r_{M,t}-r_{f,t}\) に対する感応度 \(\beta_{iM}\) として、市場ポートフォリオの分散に対する市場ポートフォリオおよび個別銘柄の共分散の比率
$$\beta_{iM}=\displaystyle{\frac{\mathrm{Cov}[r_{i,t}^e,r_{M,t}^e]}{V[r_{M,t}]}}$$
で定義されます。なお \(r_{f,t}\) はリスクフリーレートです。
2.ベータはどのように推定されるか
ベータの推定量 \({\hat{\beta}}_{iM}\) は一般に最小二乗推定量
$$\hat{\beta}_{iM}=\displaystyle{\frac{\displaystyle{\sum_{i=t-T}^{t-1}(r_{i,t}^e-\bar{r}_{i,t}^e)(r_{M,t}^e-\bar{r}_{M,t}^e)}}{\displaystyle{\sum_{j=t-T}^{t-1}(r_{M,t}^e-\bar{r}_{M,t}^e)^2}}}$$
$$\bar{r}_{M,t}^e=\displaystyle{\frac{1}{n}\sum_{j=t-T}^{t-1}r_{M,t}^e}$$
$$\bar{r}_{i,t}^e=\displaystyle{\frac{1}{n}\sum_{j=t-T}^{t-1}r_{i,t}^e}$$
を用いるのが定番です ( \(\bar{r}_{i,t}^e\) および \(\bar{r}_{M,t}^e\) はそれぞれ個別銘柄の超過リターンおよび市場ポートフォリオの超過リターンの標本平均です。)。このように過去のリターンを用いたベータの推定値は特にヒストリカル・ベータと呼ばれます。
他方でNPMでは異なる計算方法を用いてベータを推定しています。前述したようにベータは市場ポートフォリオの分散 \(V[r_{M,t}^e]\) に対する個別銘柄および市場ポートフォリオの共分散 \(\mathrm{Cov}[r_{i,t}^e,r_{M,t}^e]\) の比率で表されます。
$$\beta_{iM}=\displaystyle{\frac{\mathrm{Cov}[r_{i,t}^e,r_{M,t}^e]}{V[r_{M,t}]}}$$
これはすなわち \(V[r_{M,t}^e]\) および \(\mathrm{Cov}[r_{i,t}^e,r_{M,t}^e]\) を推定することができれば、最小二乗推定量を用いずとも定義式からベータを直接計算できることを意味します。このように市場ポートフォリオ分散の推定値および個別銘柄・市場ポートフォリオ共分散の推定値から定義により計算されたベータをファンダメンタル・ベータと呼ばれます。このとき \(V[r_{M,t}^e]\) および \(\mathrm{Cov}[r_{i,t}^e,r_{M,t}^e]\) はファクターモデルを前提として各ファクターのエクスポージャー、各ファクターのリスクおよびスペシフィックリスクから計算できます。
3.ベータはどの推定方法が良いのか
ファンダメンタル・ベータに特徴的なのは、リスクに影響を与えるであろう現時点の情報がリスクモデルのエクスポージャーを通じて与えられるという点です。NPMのリスクモデルではエクスポージャーが推定データ時点ごとにおける最新の銘柄(ポートフォリオ)の財務情報などを通じて算出され、それを基にファクターリターン(およびその分散共分散行列)を推定しています。そのため、この意味で銘柄(ポートフォリオ)の現時点における情報はエクスポージャーが直接的に保持していると考えられます。
一般にある確率変数の定数倍で新たに定義される確率変数のリスクは元の確率変数のリスクに定数の絶対値を掛けた値に等しくなります。したがってファンダメンタル・ベータはエクスポージャーの大小を通じて毎時点における現時点の情報をリスク寄与の水準に含めています 1共分散でも同様にエクスポージャーは影響を与えます。。
他方でヒストリカル・ベータは各銘柄(ポートフォリオ)の複数過去時点のリターン系列から計算されます。すなわちヒストリカル・ベータは過去のリターンが持っている現時点に関する情報を通じて与えられています。
こうした特徴を受けて、ヒストリカル・ベータとファンダメンタル・ベータのメリット・デメリットをまとめると以下のとおりです。
| メリット | デメリット | |
|---|---|---|
| ヒストリカル・ベータ | ●スプレッドシート上でも計算できる。 ●計算方法が一般に広く知られている。 | ●一般に推定値が不安定。 ●過去一定期間分のリターンが必要で上場したての銘柄では計算できない。 ●最小二乗法ではモデルに様々な仮定を置く必要がある。 |
| ファンダメンタル・ベータ | ●上場したての銘柄でも安定した計算が可能。 ●分散共分散行列を頑健に推定できれば推定値が安定する。 | ●ファクターモデルの存在が前提でないと分散共分散行列の計算が困難。 ●分散共分散行列の計算が困難。 |
このようにベータの推定方法は様々ですが、ではこれらの方法のうち、どれを用いるのが良いのでしょうか。これに対する回答を先に述べるならば、「メリット・デメリットを踏まえつつ目的に応じて使い分けよ」でしょう。
まずヒストリカル・ベータですが、様々なアプリケーションにおいて専用の計算式を(デフォルトで)内蔵しているのが一般的になっており、計算がそこまで難しくない点がメリットです。これに対してデメリットは複数あります。まず一般に推定値が不安定です。株式リターンは一般に大きく変動しやすいため、(特に最小二乗法による推定では)ベータの推定値もまた大きく変動しがちです。また過去一定期間のデータが必要です。ある程度の期間を取らなければ推定値が不安定になりますし、上場したての銘柄ではそもそもベータを推定できないという問題が発生します。
対照的にファンダメンタル・ベータは、エクスポージャーや分散共分散行列がクロスセクション・データを用いて時点ごとに推定するため、上場したての銘柄であっても多少の仮定の下である程度の安定性をもって計算することができます。また推定値の安定性は分散および共分散の安定性に依存するため、それらを頑健に推定することができれば、ベータもまた頑健に推定することができます。一方で分散共分散行列を計算するのは計算速度などの問題から一般に困難です。
これらのメリット・デメリットを確認する意味も込めて、実際の推定値を見てみましょう。以下の図1は、市場ポートフォリオをTOPIXと見なしたときのトヨタ自動車(7203)のベータを2012年1月初頭から2021年12月末までの10年分、時系列でプロットしたものです。ここでは(共)分散が時系列で安定するように設計された①NPMリスクモデルを用いたファンダメンタル・ベータと、(共)分散の変化がよりビビッドに反映されるように設計された②NPM短期リスクモデルを用いたファンダメンタル・ベータ、また③直近250営業日のデータを用いたヒストリカル・ベータおよび④直近50営業日のデータを用いたヒストリカル・ベータの計4種類のベータを準備しました。
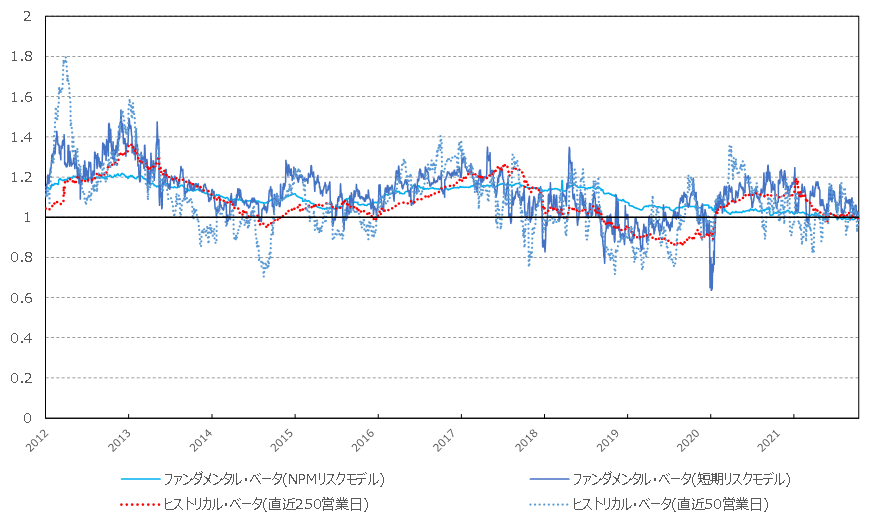

最も安定して推移したのはNPMリスクモデルで推定したファンダメンタル・ベータで、その標準偏差は0.0595と最も小さかったです。対照的に最も不安定に動いたのは、直近50営業日のデータを用いたヒストリカル・ベータで、その標準偏差は0.1704でした。
他方で、NPMリスクモデルで推定したファンダメンタル・ベータや直近250営業日のデータを用いたヒストリカル・ベータの方が他2つよりもトレンドが転換するタイミングが遅いようにも見受けられます。大きく動いたデータがあってもそれ1つが推定値に与える影響力が相対的に小さいからです。
以上から、より安定したデータを求めるのであれば、NPMリスクモデルで推定したファンダメンタル・ベータや長期間のデータを推定に用いたヒストリカル・ベータを用い、逆にリスクをより機敏に反映させたい意図があれば短期リスクモデルで推定したファンダメンタル・ベータや短期間のデータを推定に用いたヒストリカル・ベータを用いるのが望ましいと言えます。
4.まとめ
- 過去一定期間のリターンから(最小二乗法などで)直接推定したベータをヒストリカル・ベータといい、ファクターモデル(リスクモデル)を基に推定した(共)分散から計算したベータをファンダメンタル・ベータといいます。
- ヒストリカル・ベータおよびファンダメンタル・ベータにはそれぞれメリット・デメリットがあります。
- NPMで表示しているベータはファンダメンタル・ベータであり、ヒストリカル・ベータにおける意味での推計期間(直近何営業日分のデータを利用しているのか)は定義されません。
